The Fourth Dimension
GA 324a
31 March 1905, Berlin
Translated by Steiner Online Library
Second Lecture
Today I want to discuss some elementary aspects of the idea of multidimensional space [among other things, in connection with the] spirited Hinton.
You will recall how we arrived at the concept of multi-dimensional space, having considered the zeroth dimension [last time]. I would like to briefly repeat the ideas of how we can move from two- to three-dimensional space.
What do we mean by a symmetrical behavior? How do I align a red and a blue [flat figure, which are mirror images of each other]?
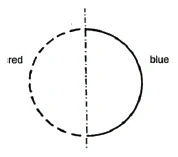
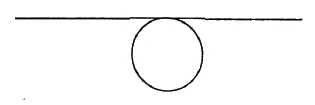
With two halves of a circle, I can do this relatively easily by sliding the red [half] circle into the blue one (Figure 10).
This is not so easy in the following [mirror]symmetrical figure (Figure 11). I cannot make the red and blue parts coincide [in the plane], no matter how I try to slide the red into the blue.
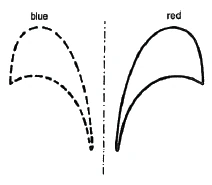
But there is a way [to achieve this anyway]: if you step out of the board, that is, out of the second dimension [and use the third dimension, in other words, if you] place the blue figure on the red one [by rotating it through the space around the mirror axis].
The same applies to a pair of gloves: I cannot match one with the other without stepping out of [three-dimensional] space. You have to go through the fourth dimension.
Last time I said that in order to develop an understanding of the fourth dimension, you have to make [the relationships in] space fluid, thereby creating conditions similar to those you have when moving from the second to the third dimension. In the last lesson, we created spatial structures out of paper strips that intertwined. Such interweaving causes certain complications. This is not a game, but such inter-weavings occur in nature all the time. Anyone who reflects on natural processes knows that such inter-weavings really do occur in nature. Material bodies move in such intertwined spatial structures. These movements are endowed with forces, so that the forces also intertwine. Take the movement of the earth around the sun and then the movement of the moon around the earth. The moon moves in an orbit that is itself wound around the earth's orbit around the sun. It thus describes a spiral around a circular line. Because of the movement of the sun, the moon describes another spiral around this. The result is very complicated lines of force that extend through the whole space.
The heavenly bodies behave in relation to each other like the intertwined strips of paper [by Simony, which we looked at last time]. We have to keep in mind that we are dealing with complicated spatial concepts that we can only understand if we do not let them become rigid. If we want to grasp space [in its essence], [we must first conceive it as rigid, but then] make it completely fluid again. [You have to go as far as zero]; the [living] point can be found in it.
Let us once again visualize the structure of the dimensions]. The point is zero-dimensional, the line is one-dimensional, the surface is two-dimensional and the body is three-dimensional. The cube has the three dimensions: height, width and depth. How do the spatial structures [of different dimensions] relate to each other? Imagine that you are a straight line, that you have only one dimension, that you can only move along a straight line. If such beings existed, what would their concept of space be like? Such beings would not perceive one-dimensionality in themselves, but would only be able to imagine points wherever they went. Because in a straight line, if we want to draw something in it, there are only points. A two-dimensional being would only encounter lines, so it would only perceive one-dimensional beings. [A three-dimensional being like] the cube would perceive two-dimensional beings, but could not perceive its [own] three dimensions.
Now, humans can perceive their three dimensions. If we reason correctly, we must say to ourselves: Just as a one-dimensional being can only perceive points, a two-dimensional being only straight lines, and a three-dimensional being only surfaces, so a being that perceives three dimensions must itself be a four-dimensional being. The fact that humans can define external beings in terms of three dimensions, can [deal with] spaces of three dimensions, means that they must be four-dimensional. And just as a cube can perceive only two dimensions and not its third, so it is clear that man cannot perceive the fourth dimension in which he lives. Thus we have shown [that man must be a four-dimensional being]. We swim in the sea [of the fourth dimension, like ice in water].
Let us return once more to the consideration of mirror images (Figure 11). This vertical line represents the cross-section of a mirror. The mirror reflects an image [of the figure on the left]. The process of reflection points beyond the two dimensions into the third dimension. [To understand the direct and continuous connection between the mirror image and the original, we have to add a third dimension to the two.
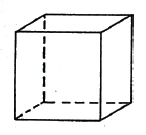
[Now let us consider the relationship between external space and internal representation.] The cube here apart from me [appears as] an idea in me (Figure 12). The idea [of the cube] is related to the cube like a' mirror image to the original. Our sensory apparatus [creates an imagined image of the cube. If you want to align this with the original cube, you have to go through the fourth dimension. Just as the third dimension has to be transitioned to (during the continuous execution of the two-dimensional) mirroring process, our sensory apparatus has to be four-dimensional if it is to be able to establish a [direct] connection [between the imagined image and the external object].
If you only imagined [two-dimensionally], you would [only] have a dream image in front of you, but you would have no idea that there is an object outside. Our imagination is a direct inversion of our ability to imagine [external objects by means of] four-dimensional space.
The human being in the astral state [during earlier stages of human evolution] was only a dreamer, he had only such ascending dream images.” He then passed from the astral realm to physical space. Thus we have mathematically defined the transition from the astral to the [physical-] material being. Before this transition occurred, the astral human being was a three-dimensional being and therefore could not extend his [two-dimensional] ideas to the objective [three-dimensional physical-material] world. But when he [himself] became physical-material, he still acquired the fourth dimension [and could therefore also experience three-dimensionally].
Due to the peculiar design of our sensory apparatus, we are able to align our perceptions with external objects. By relating our perceptions to external things, we pass through four-dimensional space, imposing the perception on the external object.
How would things appear if we could see from the other side, if we could enter into things and see them from there? To do that, we would have to pass through the fourth dimension.
The astral world itself is not a world of four dimensions. But the astral world together with its reflection in the physical world is four-dimensional. Anyone who is able to see the astral world and the physical world at the same time lives in four-dimensional space. The relationship of our physical world to the astral world is a four-dimensional one.
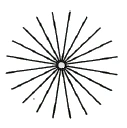
One must learn to understand the difference between a point and a sphere. In reality, this point would not be passive, but a point radiating light in all directions (Figure 13).
What would be the opposite of such a point? Just as there is an opposite to a line that goes from left to right, namely a line that goes from right to left, there is also an opposite to the point. We imagine an enormous sphere, in reality of infinite size, that radiates darkness from all sides, but now inwards (Figure 14). This sphere is the opposite of the point.
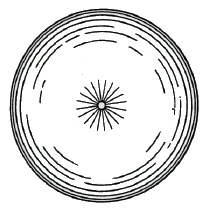
These are two real opposites: the point radiating light and infinite space, which is not a neutral dark entity, but one that floods space with darkness from all sides. [As a contrast, this results in] a source of darkness and a source of light. We know that a straight line that extends to infinity returns to the same point from the other side. Likewise, it is with a point that radiates light in all directions. This light comes back [from infinity] as its opposite, as darkness.
Now let us consider the opposite case. Take the point as the source of darkness. The opposite is a space that radiates light from all sides.
As was recently demonstrated [in the previous lecture], the point behaves in this way; it does not disappear [into infinity, it returns from the other side] (Figure 15).
[Similarly, when a point expands or radiates out, it does not lose itself in infinity; it returns from infinity as a sphere.] The sphere, the spherical, is the opposite of the point. Space lives in the point. The point is the opposite of space.
What is the opposite of a cube? Nothing other than the whole of infinite space, except for the piece that is cut out here [by the cube]. So we have to imagine the [total] cube as infinite space plus its opposite. We cannot do without polarities if we want to imagine the world as powerfully dynamic. [Only in this way] do we have things in their life.
If the occultist were to imagine the cube as red, the space around it would be green, because red is the complementary color of green. The occultist not only has simple ideas for himself, he has vivid ideas, not abstract, dead ideas. The occultist must enter into things from within himself. Our ideas are dead, while the things in the world are alive. We do not live with our abstract ideas in the things themselves. So we have to imagine the infinite space in the corresponding complementary color to the radiating star. By doing such exercises, you can train your thinking and gain confidence in how to imagine dimensions.
You know that the square is a two-dimensional spatial quantity. A square composed of four red- and blue-shaded sub-squares is a surface that radiates differently in different directions (Figure 16). The ability to radiate differently in different directions is a three-dimensional ability. So here we have the three dimensions of length, width and radiance.
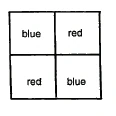
What we did here with the surface, we also think of as being done for the cube. Just as the square above was made up of four sub-squares, we can imagine the cube as being made up of eight sub-cubes (Figure 17). This initially gives us the three dimensions of height, width and depth. Within each sub-cube, we can then distinguish a specific light-emitting capacity, which results in a further dimension in addition to height, width and depth: the radiation capacity.
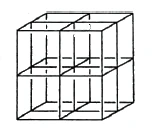
You can imagine a square made up of four sub-squares, a cube made up of eight different sub-cubes. And now imagine a body that is not a cube, but has a fourth dimension. We have created the possibility of understanding this through radiative capacity. If each [of the eight partial cubes] has a different radiating power, then if I have only the one cube that radiates only in one direction, if I want to obtain the cube that radiates in all directions, I have to add another one on the left, doubling it with an opposite one, I have to put it together out of 16 cubes.
Next lesson we will have the opportunity to consider how we can think of a multidimensional space.
Zweiter Vortrag
Heute will ich einiges Elementare über die Vorstellung des mehrdimensionalen Raumes besprechen [unter anderem in Anschluß an den] geistvollen Hinton.
Sie erinnern sich, wie wir [das letzte Mal] von der Betrachtung der nullten Dimension bis zur Vorstellung des mehrdimensionalen Raumes kamen. Ich will die Vorstellungen, wie wir vom zweizum dreidimensionalen Raum kommen können, kurz noch einmal wiederholen.
Was haben wir unter einem Symmetrie-Verhalten zu verstehen? Wie bringe ich eine rote und eine blaue [ebene Figur, die Spiegelbilder voneinander sind,] zur Deckung?

Das kann ich bei zwei Kreishälften relativ leicht, indem ich den roten [Halb-]Kreis in den blauen hineinschiebe (Figur 10).
Bei der folgenden [spiegel]symmetrischen Figur gelingt dies nicht so leicht (Figur 11). Ich kann den roten und den blauen Teil [innerhalb der Ebene] nicht zur Deckung bringen, auf welche Weise auch immer ich das Rote in das Blaue hineinzuschieben versuche.

Aber es gibt ein Mittel [dies trotzdem zu erreichen]: Wenn man aus der Tafel, das heißt aus der zweiten Dimension heraustritt [und die dritte Dimension zu Hilfe nimmt, mit anderen Worten, wenn man] die blaue Figur auf die rote legt [indem man sie durch den Raum um die Spiegelachse dreht].
Genauso verhält es sich mit einem Paar Handschuhen: Ich kann den einen mit dem anderen nicht zur Deckung bringen, ohne daß ich aus dem [dreidimensionalen] Raum heraustrete. Man muß durch die vierte Dimension gehen.
Ich habe das letzte Mal gesagt, daß man [die Beziehungen im] Raum flüssig machen muß [wenn man sich eine Vorstellung von der vierten Dimension erarbeiten will], um dadurch ähnliche Verhältnisse zuwege zu bringen, wie man sie hat, wenn man von der zweiten in die dritte Dimension übergeht. In der letzten Stunde haben wir aus Papierstreifen Raumgebilde erzeugt, die sich ineinander verschlingen. Solche Verschlingungen rufen bestimmte Komplikationen herbei. Das ist keine Spielerei, sondern in der Natur kommen fortwährend solche Verschlingungen vor. Wer nachdenkt über Naturprozesse, weiß, daß solche Verschlingungen wirklich in der Natur vorkommen. Materielle Körper bewegen sich in solchen verschlungenen Raumgebilden. Diese Bewegungen sind mit Kräften ausgestattet, so daß die Kräfte sich ebenfalls gegeneinander verschlingen. Nehmen Sie die Bewegung der Erde um die Sonne und dann die Bewegung des Mondes um die Erde. Der Mond durchläuft einen Kreis, der um den Bahnkreis der Erde um die Sonne herumgeschlungen ist. Er beschreibt also eine Schraubenlinie um eine Kreislinie. Wegen der Bewegung der Sonne macht der Mond um diese eine weitere Schraubenlinie. Es ergeben sich also sehr komplizierte Kräftelinien, die sich durch den ganzen Raum erstrecken.
Die Himmelskörper verhalten sich so zueinander wie die verschlungenen Papierstreifen [von Simony, die wir das letzte Mal betrachtet haben]. Wir müssen uns vergegenwärtigen, daß wir es mit komplizierten Raumbegriffen zu tun haben, die wir nur dann begreifen, wenn wir sie nicht starr werden lassen. Wenn wir den Raum [in seinem Wesen] begreifen wollen, [müssen wir ihn zwar zunächst starr auffassen, ihn dann aber] wieder vollständig flüssig machen. [Man muß wie] bis zur Null [gehen]; darinnen ist der [lebendige] Punkt [zu finden].
Wir vergegenwärtigen uns noch einmal fden Aufbau der Dimensionen]. Der Punkt ist nulldimensional, die Linie eindimensional, die Fläche zweidimensional und der Körper dreidimensional. So hat der Würfel die drei Dimensionen: Höhe, Breite und Tiefe. Wie verhalten sich nun die Raumgebilde [verschiedener Dimensionen] zueinander? Denken Sie sich, Sie seien eine gerade Linie, Sie hätten nur eine Dimension, Sie könnten sich nur längs einer geraden Linie bewegen. Falls es solche Wesen gäbe, wie müßte die Raumvorstellung solcher Wesen geartet sein? Solche Wesen würden die Eindimensionalität bei sich nicht wahrnehmen, sondern sie würden sich nur Punkte vorstellen können überall, wo sie auch hinkämen. Denn es gibt in der geraden Linie, wenn wir etwas in ihr zeichnen wollen, nur Punkte. Ein zweidimensionales Wesen würde nur Linien antreffen, würde also nur eindimensionale Wesen wahrnehmen. [Ein dreidimensionales Wesen wie] der Würfel würde zweidimensionale Wesen wahrnehmen, könnte aber nicht seine [eigenen] drei Dimensionen wahrnehmen.
Der Mensch nun kann seine drei Dimensionen wahrnehmen. Wenn wir richtig folgern, müssen wir uns sagen: Wie ein eindimensionales Wesen nur Punkte wahrnehmen kann, ein zweidimensionales Wesen nur Geraden und ein dreidimensionales Wesen nur Flächen, so muß ein Wesen, das drei Dimensionen wahrnimmt, selbst ein vierdimensionales Wesen sein. Dadurch, daß der Mensch äußere Wesen nach drei Dimensionen abgrenzen kann, mit Räumen aus drei Dimensionen [umgehen kann], muß er vierdimensional sein. Und ebenso, wie ein Würfel nur zwei Dimensionen wahrnehmen kann und nicht seine dritte, so ist klar, daß der Mensch die vierte Dimension, in der er lebt, nicht wahrnehmen kann. Damit haben wir gezeigt, [daß der Mensch ein vierdimensionales Wesen sein muß]. Wir schwimmen im Meere [der vierten Dimension, wie Eis in Wasser].
Wir kehren noch einmal zur Betrachtung der Spiegelbilder zurück (Figur 11). Diese senkrechte Linie stellt den Querschnitt eines Spiegels dar. Der Spiegel wirft ein Spiegelbild [der Figur auf der linken Seite] zurück. Der Spiegelungsprozeß weist über die zwei Dimensionen hinaus in die dritte Dimension. [Um den unmittelbaren und kontinuierlichen Zusammenhang des Spiegelbildes mit dem Original zu verstehen, müssen wir zu] den zwei Dimensionen eine dritte hinzunehmen.

[Nun betrachten wir das Verhältnis von Außenraum und Innenvorstellung.] Der Würfel hier außer mir [erscheint als] eine Vorstellung in mir (Figur 12). Die Vorstellung [des Würfels] verhält sich zum Würfel wie ein’ Spiegelbild zum Original. Unser Sinnesapparat [entwirft vom Würfel ein Vorstellungsbild. Will man dieses mit dem Originalwürfel] zur Deckung bringen, so muß man durch die vierte Dimension hindurchgehen. Genauso wie [beim kontinuierlichen Vollzug des zweidimensionalen] Spiegelprozesses zur dritten Dimension übergegangen werden muß, muß unser Sinnesapparat, wenn er imstande sein soll, einen [direkten] Zusammenhang [zwischen Vorstellungsbild und äußerem Gegenstand] herzustellen, vierdimensional sein.
Wenn Sie nur [zweidimensional] vorstellen würden, so würden Sie [nur] ein Traumbild vor sich haben, aber keine Ahnung davon haben, daß draußen ein Gegenstand ist. Unser Vorstellen ist ein direktes Stülpen unseres Vorstellungsvermögens über [die äußeren Gegenstände vermittels des] vierdimensionalen Raumes.
Der Mensch war im Astralzustand [während früherer Stadien der Menschheitsevolution] nur ein Träumer, er hatte nur solche aufsteigenden Traumbilder.” Er ist dann übergegangen vom Astralreich zum physischen Raum. Damit haben wir den Übergang vom astralen zum [physisch-]materiellen Wesen mathematisch definiert. Bevor dieser Übergang geschah, war der astrale Mensch ein dreidimensionales Wesen und konnte deshalb nicht seine [zweidimensionalen] Vorstellungen auf die objektive [dreidimensionale physisch-materielle] Welt ausdehnen. Aber als er [selbst] physisch[-materiell] geworden ist, hat er noch die vierte Dimension hinzubekommen [und konnte demzufolge auch dreidimensional erleben].
Durch die eigentümliche Einrichtung unseres Sinnesapparates sind wir imstande, unsere Vorstellungen mit den äußeren Gegenständen zur Deckung zu bringen. Indem wir unsere Vorstellungen auf äußere Dinge beziehen, gehen wir durch den vierdimensionalen Raum durch, stülpen die Vorstellung über den äußeren Gegenstand.
Wie würden sich die Dinge ausnehmen, wenn wir von der anderen Seite aus schauen könnten, wenn wir in die Dinge hineintreten und sie von dort aus sehen könnten? Um das zu können, müßten wir durch die vierte Dimension hindurch.
Die Astralwelt selbst ist nicht eine Welt von vier Dimensionen. Aber die astrale Welt zusammen mit ihrer Spiegelung in der physischen Welt ist vierdimensional. Wer imstande ist, die astrale Welt und die physische Welt zugleich zu überschauen, der lebt im vierdimensionalen Raum. Das Verhältnis unserer physischen Welt zur astralen ist ein vierdimensionales.
Man muß begreifen lernen den Unterschied zwischen Punkt und Sphäre. [In der Wirklichkeit] wäre dieser Punkt nicht passiv, sondern ein nach allen Seiten Licht ausstrahlender Punkt (Figur 13).

Welches wäre nun das Gegenteil eines solchen Punktes? Genauso wie es einen Gegensatz zu einer Linie gibt, die von links nach rechts geht, nämlich eine Linie, die von rechts nach links geht, so gibt es auch einen Gegensatz zum [Licht ausstrahlenden] Punkt. Wir stellen uns eine riesige, in Wirklichkeit unendlich große, Kugel vor, die von allen Seiten, aber jetzt nach innen, Dunkelheit verbreitet, Dunkelheit hereinschickt (Figur 14). Diese Kugel ist das Gegenteil des [Licht ausstrahlenden] Punktes.

Das sind zwei wirkliche Gegensätze: Der Licht ausstrahlende Punkt und der unendliche Raum, der nicht ein neutrales dunkles Gebilde ist, sondern der von allen Seiten her den Raum mit Dunkelheit überflutet. [Als Gegensatz ergibt sich so] eine Quelle der Dunkelheit und eine Quelle des Lichts. Wir wissen, daß eine gerade Linie, die sich in die Unendlichkeit verliert, von der anderen Seite nach demselben Punkt zurückkehrt. Ebenso ist es bei einem Punkte, der nach allen Seiten Licht ausstrahlt. Dieses Licht kommt [aus der Unendlichkeit] als sein Gegenteil, als Dunkelheit zurück.
Nun betrachten wir den umgekehrten Fall. Nehmen Sie den Punkt als Quelle der Dunkelheit. Als Gegensatz ergibt sich ein Raum, der von allen Seiten Helle hereinstrahlt.
So wie dies neulich [im vorangehenden Vortrag] durchgenommen wurde, so verhält es sich mit dem Punkt; er verliert sich nicht [in der Unendlichkeit, er kommt von der anderen Seite wieder zurück] (Figur 15).

[Ganz entsprechend verliert sich ein Punkt, wenn er sich ausdehnt oder hinausstrahlt, nicht im Unendlichen; er kommt als Sphäre aus dem Unendlichen zurück.] Die Sphäre, das Kugelförmige, ist das Gegenteil des Punktes. Im Punkte lebt der Raum. Der Punkt ist das Gegenteil des Raumes.
Was ist [das Gegenteil] eines Würfels? Nichts anderes als der ganze unendliche Raum, abgerechnet das Stück, das hier [durch den Würfel] herausgeschnitten ist. So daß wir uns den [totalen] Würfel als unendlichen Raum vorstellen müssen plus sein Gegenteil. Ohne Polaritäten kommen wir nicht aus, wenn wir uns die Welt kraftvoll dynamisch vorstellen [wollen]. [Erst so] haben wir die Dinge in ihrem Leben.
Würde sich der Okkultist den Würfel rot vorstellen, so würde der [übrige] Raum grün sein, denn Rot ist die Gegenfarbe von Grün. Der Okkultist hat nicht nur einfach Vorstellungen für sich selbst, er hat lebendige Vorstellungen, keine abstrakten, toten Vorstellungen. Der Okkultist muß aus sich heraus in die Dinge hineinkommen. Unsere Vorstellungen sind tot, während die Dinge in der Welt lebendig sind. Wir leben mit unseren abstrakten Vorstellungen nicht in den Dingen selber. So müssen wir uns zum Licht ausstrahlenden Stern den unendlichen Raum in der entsprechenden Ergänzungsfarbe hinzu vorstellen. Wenn man solche Übungen macht, kann man sein Denken schulen, bekommt man Vertrauen, wie man sich Dimensionen vorstellen kann.
Sie wissen, daß das Quadrat eine zweidimensionale Raumgröße ist. Ein Quadrat, zusammengesetzt aus vier rot- und blauschattierten Teilquadraten, ist eine Fläche, die in verschiedene Richtungen verschieden strahlt (Figur 16). Die Fähigkeit, in verschiedene Richtungen verschieden zu strahlen, ist eine dreidimensionale Fähigkeit. Wir haben hier also die drei Dimensionen Länge, Breite und Strahlungsvermögen.

Was wir hier mit der Fläche machten, denken wir uns auch für den Würfel ausgeführt. Ebenso wie das obige Quadrat aus vier Teilquadraten aufgebaut war, denken wir uns den Würfel aus acht Teilwürfeln aufgebaut (Figur 17). Daraus ergeben sich zunächst die drei Dimensionen Höhe, Breite und Tiefe. Innerhalb jedes [Teil-]Würfels wäre dann zu unterscheiden ein bestimmtes Lichtausstrahlungsvermögen, Daraus ergibt sich zusätzlich zur Höhe, Breite und Tiefe eine weitere Dimension: das Strahlungsvermögen.

Sie können sich ein Quadrat aus vier Teilquadraten zusammengefügt denken, einen Würfel aus acht verschiedenen Teilwürfeln. Und nun denken Sie sich einen Körper, der nicht Würfel ist, sondern der eine vierte Dimension hat. Wir haben uns die Möglichkeit geschaffen, dies zu verstehen durch das Strahlungsvermögen. Hat jeder [der acht Teilwürfel] ein verschiedenes Strahlungsvermögen, so muß ich, wenn ich bloß den einen Würfel habe, der ein Strahlungsvermögen nur nach einer Seite hat, wenn ich den Würfel erhalten will, der nach allen Seiten strahlt, überall zu dem linksstehenden einen anderen noch hinzufügen, ihn mit einem entgegengesetzten verdoppeln, ich muß ihn aus 16 Würfeln zusammensetzen.
Nächste Stunde werden wir die Möglichkeit bekommen, wie wir uns einen mehrdimensionalen Raum denken können.

